Deductive Reasoning (for Math Word Problem Solving)
Introduction
Large-scale pretrained language models GPT-3, have been achieving promising results on many NLP downstream tasks. However, most of these models are not able to give us the reasoning steps and the performance on the tasks require complex reasoning is still unsatisfactory (Bengio et al., 2021). We propose a deductive reasoning approach and aim to achieve the reasoning ability as in System 2 (Daniel 2017).

This paper is accepted by the 60th Annual Meeting of the Association for Computational Linguistics (ACL-2022)
Paper link : https://arxiv.org/abs/2203.10316
Research Motivation
We use the following figure taken from the PaLM (Chowdhery et al., 2022) paper as an example. This work performs prompting to solve the math word problem in a few-shot learning scenario. We can see if we give some samples with just questions and answers, we might not be able to obtain the correct answer. But if we give some more reasoning description, the model is able to predict reasoning description and also make a correct prediction. So it is good to have interpretable multi-step reasoning as output.

Also, math word problem (MWP) solving is a straightforward application to evaluate such multi-step reasoning ability.
Problem Description
Given a question, we need to solve the questions and obtain the numerical answer. In our dataset, we are also given the mathematical expression which leads to the corresponding answer.
Question: In a division sum , the remainder is \(8\) and the divisor is \(6\) times the quotient and is obtained by adding \(3\) to the thrice of the remainder. What is the dividend?
Answer: \(129.5\)
Mathematical Expression: \(\big ( {\textcolor{electronblue}{(8\times 3 + 3)}}\! \times \! {\textcolor{electronblue}{(8 \times 3 + 3)}} \!\div\! 6\big )\! +\! 8\)
This example is taken from the MathQA (Amini et al., 2019) dataset. We need to obtain the final dividend 129.5. The mathematical expression can be used for training supervision.
Existing Methods
Existing work in MWP is mainly categorized into Seq2Seq and Seq2Tree. Traditional Seq2Seq models basically are pretty easy to implement and generalize to more complicated problems. But the disadvantages are that the performance is generally not better than the structured model and it is lack of interpretability. This line of research is still popular because of Transformers-based models which potentially have powerful language understanding ability.
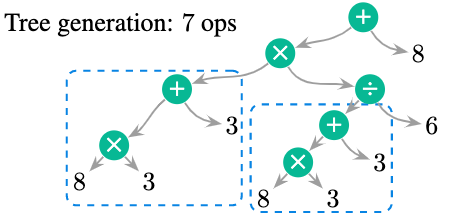
The typical approach of Seq2Tree is the Goal-Driven Tree-Structure (GTS) (Xie et al., 2019), which is also the most common work that followed by other research efforts on MWP. In tree-based generation models, we structure the expression in tree form and follow a pre-order traversal in tree generation as shown in the Figure below. We keep generating the operators until we reach the leaves which are the quantities.
The Nice thing is that it gives us a binary tree structure, but it is also counter-intuitive and contains repetitive computations. Take these two blue and dashed boxes for instance, we can see this expression \(8\times 3+3\) is generated twice, but we can actually reuse it without generating it again. Under the Seq2Tree framework, we are not able to do so.
Deductive Reasoning
In our proposed approach, we want to solve this problem in a step-by-step and interpretable manner as shown in the Figure below.
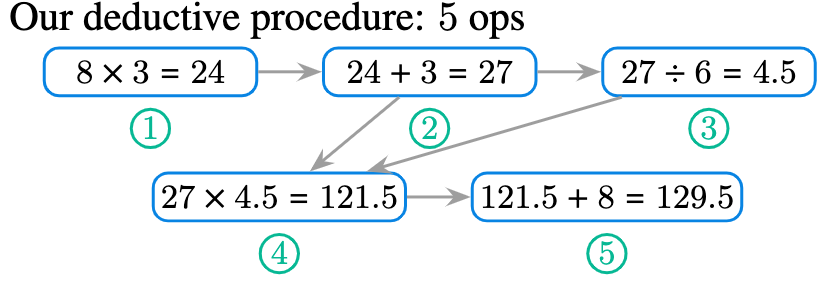
The first two steps give us the divisor. The third step computes the quotient. We can see that the results of the first two steps can be used at the fourth step for the final dividend computation.
Overall, our deductive procedure has the following advantages:
- Reduce the number of computation steps by reusing the previous expressions.
- More explanability with step-by-step expression computation
- Generating the complete expression rather than a single operator or quantity. Such a process requires the model to be more accurate during training.
In addition, similar to diffusion models, we can actually start from the intermediate step and continue to perform inference at the intermediate step.
Deductive Systems
Model Input: the quantities presented in the question and the complete constant set, which is represented by \(Q\).
\[Q=Q^{(t=0)}= \{ q_1, q_2, \cdots,q_m \}\]Expressions are represented by:
\[e_{i,j,op}^{(t)} = q_i \xrightarrow[]{op} q_j ~~~q_i, q_j \in \mathcal{Q}^{(t-1)}\]Indicate the mathematical operations from \(q_i\) to \(q_j\). The underlying representation \(e_{i,j,op}^{(t)}\) is directed. For those non-commutative operators, such as subtraction and division, we use an additional reverse direction to represent such operators. Here we can use “\(-_{reverse}\)” to represent \(q_j - q_i\).
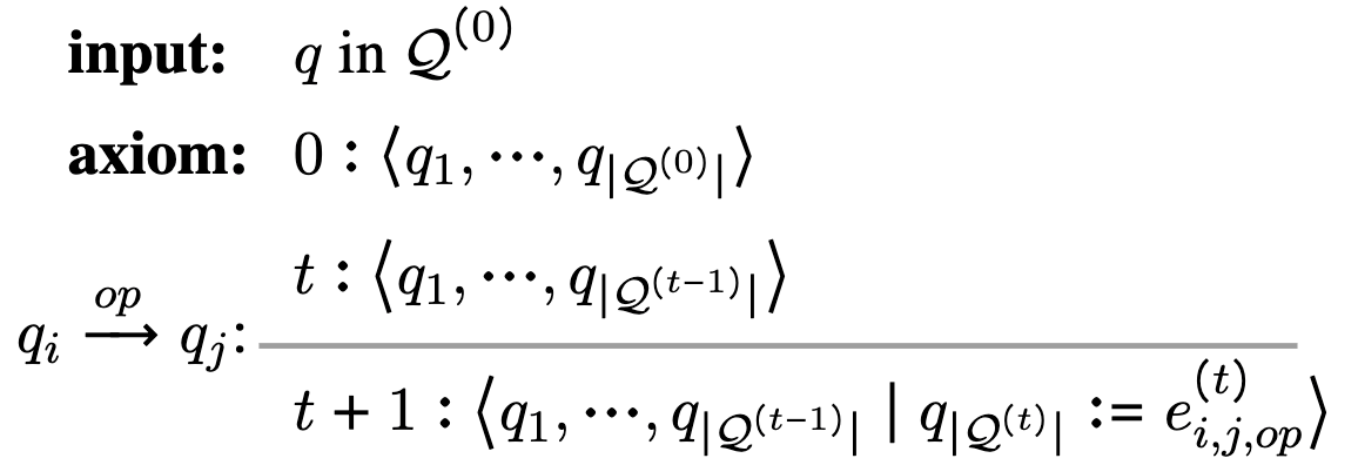
From the perspective of formal deductive systems, we can use the above derivation to represent the procedure. Such deductive process is similar to the transition-based system in dependency parsing task. From time \(t\) to \(t+1\), the difference between states is an additional new expression \(e_{i,j,op}^{(t)}\), and this new expression will be a new candidate quantity at the next state.
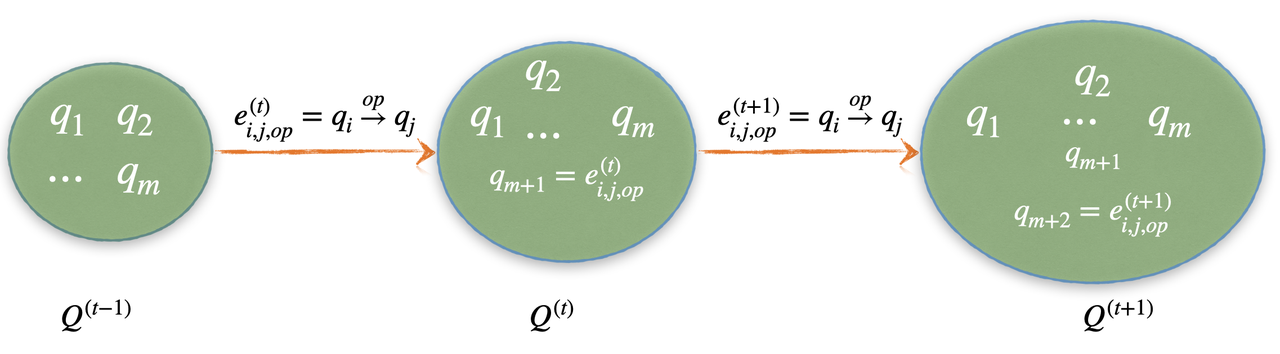
The above figure visualizes the evolution of the states. We can see that, we size of the state increases with the increase of time step \(t\).
Model Implementation
First, we use pre-trained language models such as BERT or Roberta to obtain vector representation of quantities. We then perform inference on top of these quantity representations. Here, we use an example to visualize the inference process.
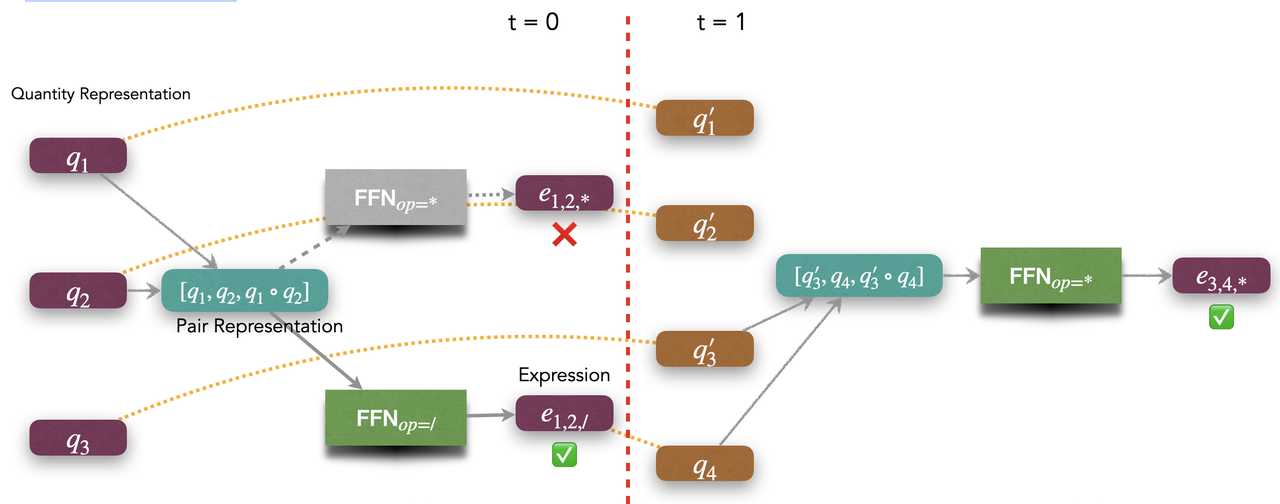
At the first step, we obtain the joint representation between and by simple concatenation between their quantity representations. We then apply an operator-specific feed-forward network to obtain the vector representation of the mathematical expression . Thus, this new expression will become the new candidate quantity . Potentially, we might obtain incorrect expressions, such as . Thus, we need to score all the possible expressions and find the optimal expression to be the new quantity . Finally, at , we arrive at the expression .
One of the advantages of this implementation is that we can incorporate prior knowledge as constraints. For example, if the expression is not allowed, we can simply remove this expression from the candidate set.
Note that, the number of all the possible candidates at different timestep is different. This actually makes it challenging for us to perform beam search during inference. Because the probability distribution at different time steps will be unbalanced.
Experiments
We mainly conduct experiments on four public datasets: MAWPS, Math23k, MathQA and SVAMP. In this blog, we just show the comparison with the state-of-the-art approaches under the same setting (i.e., using BERT/Roberta language models.). Our best variant is the Roberta-Deductive Reasoner and we did not apply the beam search strategy. The compared approaches are all using beam search with beam size of 5.
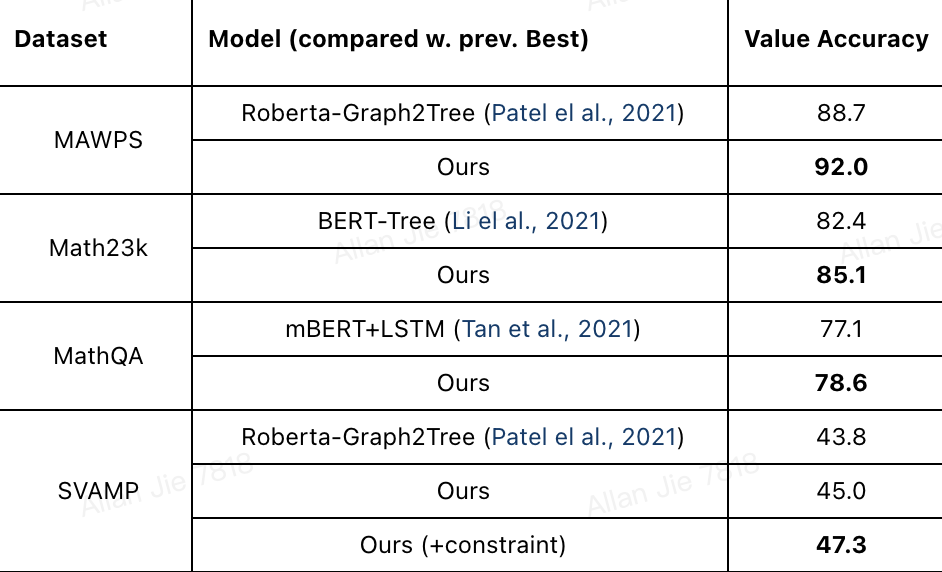
Overall, our accuracy on the final numerical answer is significantly better than previous Seq2Tree work. We mainly attribute the reason to the fact that we enforce the model to predict the complete expression rather than a single operator or quantity. However, the absolute accuracy is not really high, especially on MathQA and SVAMP.
We further conduct analysis to investigate the difficulties in SVAMP. Details can be found in the paper. We found that the constraint introduced above has significantly improved the performance on the SVAMP dataset. The constraint is simply disallowing the appearance of negative values. This constraint improves our BERT-based Reasoner by 7 points and 2 points for Roberta-based Reasoner.
Interpretable Analysis
In this example, we would like to showcase how we can interpret the model predictions.
Question: There are 255 apple trees in the orchard. Planting another 35 pear trees makes the number exactly the same as the apple trees. If every 20 pear trees are planted in a row, how many rows can be planted in total?
Answer: 11. Gold Expression: \((255 - 35) \div 20\). Predicted Expression: \((255 + 35) \div 20\)
Deductive Scores: Prob('255+35=290') = 0.068 > Prob('255-35=220') = 0.062
At the first step of prediction, we can see the model make a mistake by predicting the subtraction as addition. The error can be actually located by the sentence marked in red. We suspect that the "planting another" statement misleads the model to make an "addition" prediction. We then want to revise that sentence and make it convey more accurate semantics. The italic sentence below is the revised sentence.
Question: There are 255 apple trees in the orchard. The number of pear trees is 35 fewer than the apple trees. If every 20 pear trees are planted in a row, how many rows can be planted in total?_
Prob(255+35=290) = 0.061 < Prob(255-35=220) = 0.067
Through the word "fewer", we hope the model understands that this part should be a subtraction. This study shows how interpretable predictions help us understand our model behavior.
Conclusions
Our deductive system is structurally more efficient compared to the tree-based model and is able to provide explainable solving steps. Furthermore, we are able to incorporate prior knowledge as constraints to improve the model performance. Theoretically, the underlying deductive system can not only apply to math word problem solving but also other tasks that require multi-step reasoning and structure predictions.
We also have certain limitations under this framework: the memory consumption is high when we have many mathematical operators and constants. In addition, it is still challenging to efficiently apply beam search in our framework because of the unbalanced distribution at each time step.
References
Bengio, Yoshua, Yann Lecun, and Geoffrey Hinton. "Deep learning for AI." Communications of the ACM 64.7 (2021): 58-65.
Daniel, Kahneman. "Thinking, fast and slow." (2017).
Chowdhery, Aakanksha, et al. "Palm: Scaling language modeling with pathways." arXiv preprint arXiv:2204.02311 (2022).
Amini, Aida, et al. "MathQA: Towards Interpretable Math Word Problem Solving with Operation-Based Formalisms." Proceedings of NAACL, 2019.
Xie, Zhipeng, and Shichao Sun. "A Goal-Driven Tree-Structured Neural Model for Math Word Problems." Proceedings of IJCAI. 2019.